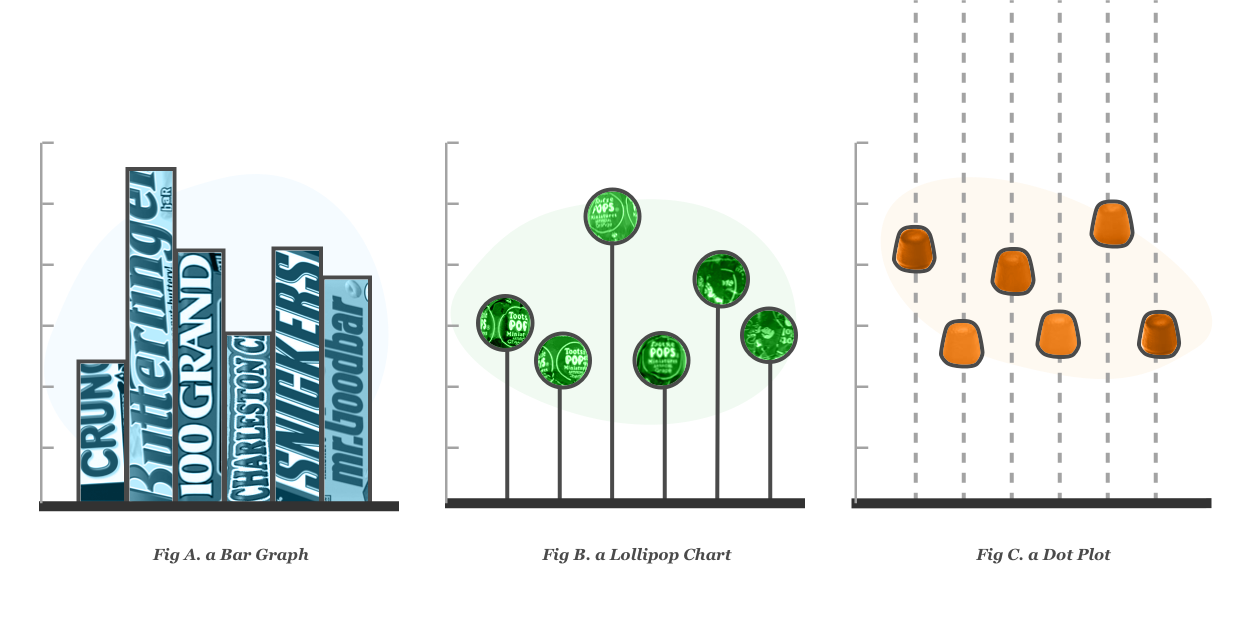
Introduction
In 2017, some people were arguing on the internet. Notably, a few of them were thoughtful characters in the data visualization community, such as Stephen Few, Andy Cotgreave, Alberto Cairo, and Jeffrey Shaffer, to name a few.
The topic: What’s the value of a Lollipop chart? Is there something to the aesthetic (per Andy’s point)? Is the extra white space between symbols easier on our eyes (per Alberto)? Or are Lollipop charts just a “less effective version of a bar graph,” inspired by “the same thing that has inspired so many silly graphs: a desire for cuteness and novelty” (per Stephen)?
The discussion takes place in the comments on Stephen’s blog. Andy responds inline and with a post of his own. And, recently, Hicham Bou Habib summarized the discussion on Twitter, which is how I first discovered the controversy. (Thanks, Hicham!)
The debate unfolded over 24 days, from May 17 to June 10, 2017. The comments totaled about 10,000 words in response to a 400 word blog post.
Why not just test it?
What stood out to me: Why not just test it out? What’s the opportunity cost for these smart folks to hash out the pros-and-cons of two very similar visualizations? Is it more or less than the $100 it costs to push a test to a crowd-source, micro-task platform like Mechanical Turk? (Actually, yes, probably, because it’s a great discussion, but in practice …).
Stephen addressed this indirectly in the comments:
“There is still much about data visualization that we don’t understand. Shouldn’t we be spending most of our time exploring the unknown where the greatest potential discoveries exist rather than wasting our time covering the same well-known territory over and over again?”
To which I say: no, no, let’s test the silly dataviz … for fun?!
So, can we settle this high-stakes, life-or-death, “bar vs. lollipop” controversy with Mechanical Turk? This is an attempt to find out. As an added bonus, per Hicham’s and Alberto’s suggestions on Twitter, I also added a last minute variant for dot plots, in hopes of actually learning something useful.
Read below for the results of my grand experiment.
What are we hoping to learn here?
Some questions raised by the discussion:
- To Stephen’s main objection: How do lollipop charts affect readers’ comprehension? How much of our epistemic responsibility are we sacrificing for a playful aesthetic?
- Is there any significant difference at all?
- Is one of the designs more “glanceable” than the other? (i.e. can it be comprehended more quickly?)
- For which use cases might bars outperform lollipops (or vice versa)?
- Might dot plots be a more reasonable solution than either of the above?
Experimental Setup
To test the above, I gave ~150 Mechanical Turkers a simple quiz, asking them to answer questions based on different graphs.
(When I’ve looked at similar studies, seeing the prompts and questions for myself always makes the experiment clearer, so I’ve put an example of the “quiz” in this Observable notebook: Bars vs. Lollipops vs. Dots: Sample Prompt Questions).
The goal of the quiz was not to test the participants, of course, but to test the visualizations within the quiz, to see if one of the three different chart types results in more accurate or faster comprehension.
Each participant was shown a quiz consisting of the same 21 questions. The questions were divided into three different sections, where each section had a different chart that the questions referred to (the first was about bake sale results, the second was student grades on a quiz and the last was teacher salaries).
Behind the scenes, each participant was randomly assigned to one of three experimental groups, one for each of the three chart types: Bar Graphs, Lollipop Charts, and Dot Plots. You can see the three variants in the image above. All the charts presented in a given quiz were the same type (i.e. a participant would see all bar graphs, or all dot plots, or all lollipops, and not a mixture of different chart types).
Each section’s chart was based on a randomly generated, normally distributed dataset to control for possible advantages that a given chart type might have with different shapes of data (e.g. in the original blog post’s comments, someone hypothesized that lollipop charts might have an advantage when the underlying data was uniformly far from 0).
To measure comprehension time, timestamps were recorded for when participants answered each question, to give a rough sense of the time spent on each answer. This was not a perfect way to measure timing, but should still give some relative signal between the variants.
The Questions
To evaluate different use cases, workers were asked a variety of questions across five different question types. Similar to Saket & friends’ 2015 paper, the question types covered a different tasks ranging from simply retrieving values (e.g. “How many Donuts did Mr. Brown’s class sell during the bake sale?”) through summarizing the “gist” of the presented data (e.g. “How many cookies did the teams sell on average?”).
Example “question types” and questions:
- Retrieval: “How many Donuts did Mr. Brown’s class sell?”
- Extremes: “For the class that sold the least cookies, how many cookies did they sell?”
- Gist: “What was the average quiz score for all students?”
- Differences: “How much higher (or lower) was Fran’s vs. Freddy’s score?”
- Filtering: “How many students scored at least 90% on the quiz?”
To minimize issues with numeracy or graph literacy, the questions were kept very simple. “Harder” questions like prediction or inference were avoided (src). To explore differences in answer types, some questions were multiple choice and some were numeric.
The Measures
To evaluate accuracy, I used two different measures: “Error” for numeric questions and binary “Correctness” for multiple choice questions. To evaluate comprehension time, I measured “Time” between answers. For each of these, see more details on calculations in the “Analysis Notes” below.
Error: For numeric question accuracy (e.g. “How many Cookies sold?“) I calculated each answer’s “error,” or the difference between the correct answer and the user’s answer (similar to Heer & Bostock, Cleveland & McGill). This ensures more granular variation across answers, making it easier to detect smaller differences in accuracy.
Correctness: For multiple-choice question accuracy (e.g. “Which class sold the most Cookies?”), I assigned correct answers a “1” and incorrect answers a “0,” so that the mean of 1s and 0s is the percent correct (similar to Saket & friends). While this allows less granular differences in answers, it fits more naturally with categorical answers for “gist” questions (e.g. “which class?”, “which teacher?”, etc).
Time: To measure response times, I calculated the difference between an answer’s timestamp and the timestamp of the previous answer.
The Results
After all the fuss, the results show no significant differences between Bar and Lollipop graphs. They led to roughly equal accuracy and equal response times.
There were, however, significant differences between Dot Plots and the other two chart types.
Participants answered more accurately, or with significantly less error, on numerical questions when presented with Dot Plots vs. Bar Graphs (p < 0.001). Even though there were significant differences between the “best” (dot plots) and the “worst” (bar graphs), the intermediate differences were not significant (i.e. there were no significant differences between Dot Plots and Lollipops, or between Lollipops and Bar Graphs). There were also no significant error differences between any of the three charts on the multiple choice questions.
Testers also answered significantly faster when presented with Lollipop Charts vs. Dot Plots (p<0.05). They answered questions most quickly when presented with Lollipops, but there were no significant response-time differences between Lollipops and Bar Graphs, or between Bar Graphs and Dot Plots.
But the effect sizes …
One important note: Just because a difference is significant, doesn’t mean that it’s meaningful. Between the three chart variants, the best one was only ~1% more accurate on average than the worst (e.g. on a chart where the Y-Axis is 0–100%, this is equivalent to mistaking 71 for 72). And the fastest chart was ~1 second faster than the slowest.
Task-Specific Results
Task-specific results were consistent with overall results.
For accuracy, there were statistically significant effects for two question types: “Retrieval” (F(2,543)=4.871; p=0.008; η2=0.018) and “Difference” (F(2,393)=5.264; p=0.006; η2=0.026). For Retrieval, Dot Plots showed significantly less error than Bars or Lollipops (p<0.01). For Differences, Dot Plots led to significantly less error than Bar Graphs, but there were no significant differences between Dots and Lollipops or Lollipops and Bars.
For speed, there was a statistically significant effect only for “Gist” question types (F(2,813)=3.454; p=0.032; η2=0.008). However, post-hoc tests did not confirm this, showing no significant, task-related differences between any pair of variants (Tukey’s HSD test, or ”Honestly Significant Difference test,” is known to be “conservative,” which may explain the discrepancy).
User Preferences
Finally, the experiment looked at two other questions: 1) Which of the chart variants do people prefer? And 2), perhaps most critically, which of the listed bake sale treats do participants prefer?
When asked “how effective were the above charts in presenting the data?” users rated Lollipop charts as the most effective on a 5-point scale. This difference was not significant though.
Troublingly, a plurality of respondents (42%) reported that Brownies were their favorite treat. Most concerning: Cupcakes, the obviously superior snack, were the least frequently preferred treat. Unfortunately, this departure from objective snack reality calls into question the validity of the entire study. As such, I encourage readers to examine the Experimental Setup and Analysis Notes carefully and tell me where I went wrong.
Analysis Notes
Of the 150 workers who submitted answers, I omitted nine. Even though the Mechanical Turk Worker selection criteria was set to 95% HIT acceptance (or 95% of their previous ”Human Intelligence Tasks” were accepted by previous requestors), not all submissions seemed to be done in good faith. I did not require a screening exercise (per Heer and Bostock or Saket & friends), instead I removed workers after-the-fact based on one or more of the following conditions: average numeric errors were more than 20% incorrect, whose multiple choice answers were less than 25% correct, or who had previously participated in practice runs of the survey. I also omitted 52 answers (1.7% of 2,898) where error was greater than 50%, assuming mistakes of this magnitude are due to something other than the graphs themselves.
Error was calculated as:
log2(| 100 * (
expected_value-answer_value) /max_value| + 1/8)
where expected_value is the correct answer, answer_value is the worker’s answer and max_value is the largest value shown on the randomly generated graph.
This is based on Heer & Bostock, Cleveland & McGill’s error formulas, with additional terms for scaling to 100%, since the 3 question-sets’ graphs have different ranges of values (see the question sets here, for context).
Taking the log of the absolute error helps transform the data into a more normal distribution, friendlier for ANOVA / F-Testing. The ⅛ term is used because log2 gets squirrely at zero.
Timing was calculated as:
log2(
answer_timestamp-previous_answer_timestamp)
where answer_timestamp is the last time a user changed the related answer field on the survey form and previous_answer_timestamp is the previously most-recent time a user answered any other question (since some users answer questions out of order). Again, log2 transformation makes the values more normal for significance tests.
Both measures were evaluated at log scale, but confidence intervals above are reported after back-transforming the results into the more readable original scale. All means are mid-means.
Takeaways:
- “Why not dot plots?” This was my first time working with a dot plot in practice. As the most accurate variant, clearly they have some benefits …
- There were no significant differences between Bar and Lollipop Charts.
- Don’t stress about “best.” These three charts are certainly different visually, but in front of users that didn’t amount to much. If the difference between the “best” and the “worst” is only 1–2%, and you’re not working on medical devices or launching rockets, then it’s probably not worth stressing too much about which chart is “best.” If Lollipop charts fit the aesthetic you’re aiming for, then enjoy the lollipops.
- If you are working on medical devices or launching rockets, you should be wary of theory in a slightly different way. As Heer and Bostock note in “Crowdsourcing Graphical Perception” because visualizations are a combination of many parts that can interact in sometimes unpredictable ways, there’s only so much you can extrapolate from first-principles (or even other people’s empirical evidence). There’s no substitute for testing data visualizations with real users.